Contact angle measurements with an optical tensiometer can be quick, non-destructive, and straightforward measurements to characterize surface chemistry and understand the interaction of a surface with a liquid of interest. Young’s equation (Figure 1A) defines the measured contact angle as a function of the surface tension of the liquid, the surface energy of the solid, and the interfacial tension between the two. For this equation to be accurate, the surface needs to be ideal: rigid, insoluble, unreactive, chemically homogenous, and smooth. While reasonable assumptions and choices can be made to ensure optimal rigidity, solubility, reactivity, and chemical homogeneity, real surfaces will have some roughness. So, how does the surface roughness affect contact angle measurements, and what can be done to account for the roughness?
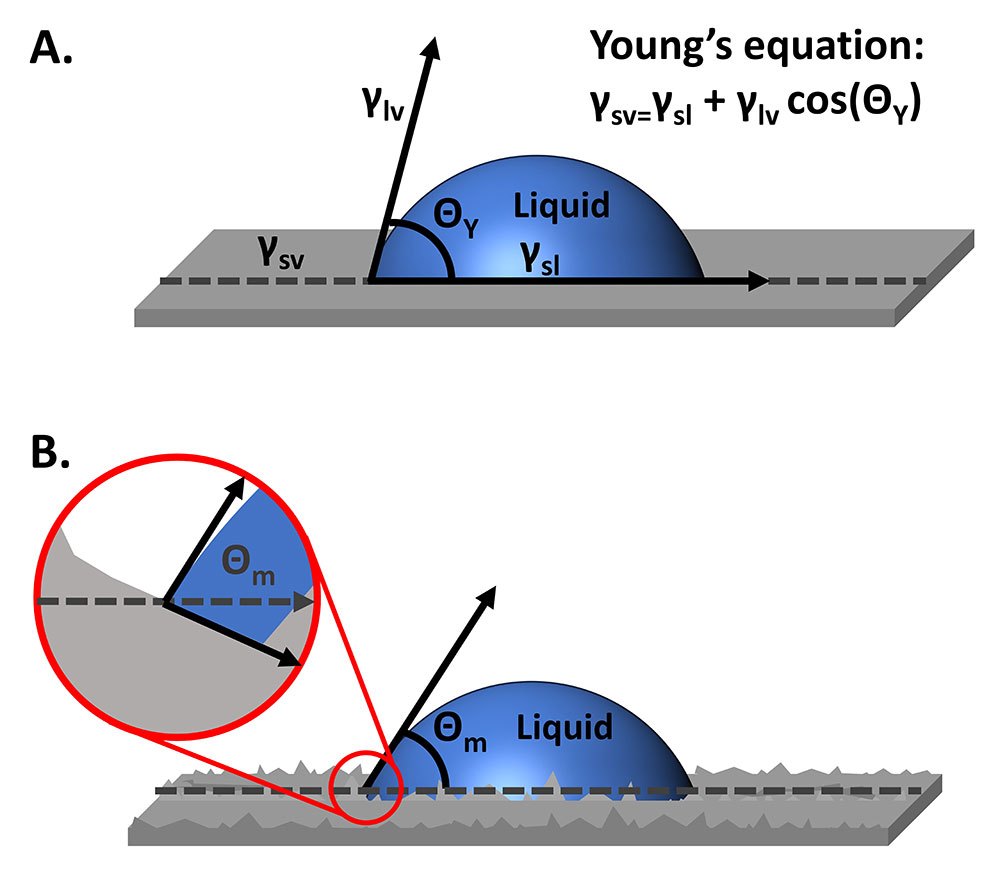
To measure contact angles using an optical tensiometer, a liquid droplet is placed onto a solid sample surface, an image of the droplet sitting on the solid is recorded, and the angles at the edges of the droplet are measured. With our ideal surface (Figure 1A), the contact angle that is measured is the Young’s or equilibrium angle. But when we move to a real surface, the measured or apparent contact angle differs from the true equilibrium contact angle. In Figure 1B, the measured contact angle, Θm, is smaller than the equilibrium contact angle that is tangent to the surface feature on which the contact line rests.

The Wenzel Model
To separate the surface roughness component of the contact angle and correct the difference in the measured contact angle and the equilibrium contact angle, the Wenzel model is commonly used [1].
cos θm = r cos θe
In the Wenzel model, our measured contact angle Θm is proportional to the equilibrium contact angle Θe by a factor of r. Here, r is equal to one plus the ratio between the exposed surface area and projected flat area (Sdr) for a given section. For a perfectly smooth surface, the exposed area is equal to the projected area, so r = 1, and the measured contact angle is equal to the equilibrium contact angle. But as the exposed area ratio increases, so does the difference between the measured and equilibrium contact angles. An interesting result of the Wenzel equation is that it always corrects the angle towards 90 degrees. In other words, roughness exaggerates the wetting or nonwetting behavior of a surface. If we place water on a hydrophobic sample, increasing the roughness makes the contact angle increase and the surface appear more hydrophobic, with the same trend for a hydrophilic surface: increasing the roughness causes the contact angle to decrease and the surface to appear more hydrophilic.
While the Wenzel model was first defined in 1936, it is still practically very useful for a large variety of surfaces like paper, wood, polymers, and even rough metallic surfaces. However, there are some conditions that must be met for it to properly apply: the liquid must fully penetrate the surface topography (no trapped air beneath the liquid) and the droplet size should be larger (2-3 orders of magnitude) than the roughness features. Assuming microliter-sized droplets that are millimeters in diameter, this lends itself well to micron or 10s of microns level roughness.
Tensiometer Solutions for Roughness Effects: Theta Flow/Flex with 3-D Topography
The Theta Flow or Flex optical tensiometers coupled with the 3-D topography module is the only tensiometer that can measure the roughness of a sample surface at the exact location of the droplet placement and then automatically correct the contact angle. By measuring the surface topography at the same location of the droplet and calculating the r-value, variations in roughness across the sample surface are mitigated, giving the most accurate and truest contact angle possible. This optical tensiometer package provides a solution for users who want to discriminate the effects of surface roughness from surface chemistry in an easy and fully automated manner.
Conclusion
While real samples can have a surface roughness that obfuscates surface chemistry as measured by contact angle, this doesn’t have to be the case. By applying a roughness correction like the Wenzel model, the equilibrium contact angle can be approximated and decoupled from a surface’s topography. There are a few assumptions that still need to be applied, but the Wenzel model is a practical solution and made instantly available with the Theta Flow/Flex tensiometers with the 3D topography model.
Related: Roughness-Corrected Contact Angle with The Attension® 3D Topography Module
References
[1] R. W. Wenzel, “Resistance of solid surfaces to wetting by water”, Ind. Eng. Chem., vol. 28, no. 8, 988-994, 1936, doi: 10.1021/ie50320a02.








